Going full circle completing the square

I usually use the last six week of the school year in geometry to teach circles: Arc lengths, chords, secants, tangents, etc. Which I have outlined in the Geometry Planning Guide

The following school year students begin Algebra 2 and promptly forget these properties of circles. They also start the new school year frustrated and overwhelmed because they forgot all about the quadratics they learned in Algebra 1 during their year in geometry.

This school year I decided to make some changes to the last unit in order to set students up to be more successful in the transition from Geometry to Algebra 2:

1)   I began with a modified version of Fawn’s task: When I got them to beg

I distributed an index card to each student and gave them students 5 minutes to make a beautiful work of art on the card. When time was up, students turned in their art, I shuffled the cards and redistributed them to the class.

I cut orange paper to the same size as 3×5 inch index cards, and told the students it was “Real Gold” it was very expensive and we could not waste any of it (they referred to orange paper as “Gold” for the rest of the school year). They had to try to make a frame for the art and tape it down to the assignment sheet that I distributed to them with an explanation of their thinking and strategy.

It worked. They begged me to help them find a better way to complete this task.

2)  Complete the Square with algebra tiles.

I used this activity from Salt Lake City Schools to guide student thinking. Students worked in small groups to create squares using algebra tiles and relating the squared and factored forms of perfect square quadratic equations. We referred back to this task often throughout the unit.

3) Solving equations by Completing the square notes and practice

I used Sarah Hagan’s foldable for completing the square. The following day I planned a basic practice sheet for students to just build fluency with solving equations by completing the square, but it was so nice out, we decided to do this on the sidewalk instead. (Note: Always keep sidewalk chalk in your classroom for beautiful day emergencies)

4) Applications of completing the square

I returned students framed art task from day 1 above, and they wrote and equation and  found the appropriate frame size using completing the square, then measured their estimated solution and reflected on their work.

Next we completed the Shell center task: Cutting Corners

5) Connecting Quadratic equations to Parabolas

I printed and laminated sets of the domino cards from the Shell Center task: Representing Quadratic Functions Graphically and students completed the loop and filled in the blanks. They then were able to summarize the relationship between standard, vertex and factored form of a quadratic equation and understand what each of the forms of the equation illustrated about it’s graph.

The next day, students worked on the Desmos Activity: Match My Parabola. I was able to pause and pace this activity as needed and monitor students understanding in order to support students understanding of the various forms of a quadratic equation.

6) Converting a quadratic equation between vertex, standard and factored forms

Now that students understood the usefulness of the various forms of quadratic equations, they wanted to be able to convert a quadratic equation between the various forms:

This slideshow requires JavaScript.

6) Develop the equation of a circle

I started with this question:

There were a few students who shouted out “Pythagorean Theorem!” and students realized they could construct a right triangle and find the length of the hypotenuse/radius.

Next, I gave students individual whiteboards and asked them to draw a circle centered at (0,0) with a radius of 5. Then I asked them to name coordinates of points that they know for sure were on the circle and I would have them explain how they knew. Eventually we identified 12 points on the circle.

After this, I asked students what the relationship was between the x and y coordinates on the circle. Most groups were able to explain that they were all related by the Pythagorean theorem because x² + y² = 5².

At this point, I had students complete the first side of the “Going Round in Circles” sheet from this Shell Center lesson in order to see how well students understood the discussion and to see how they could apply their learning.

The next class period began by asking students to find the radius of a circle given the coordinates of the center and a point:

The vertical height of the right triangle should be 12, not 13! This was corrected during the class discussion.

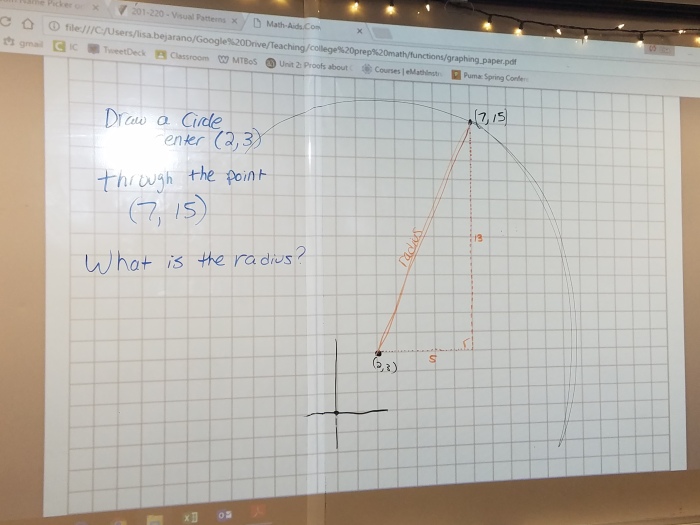
We used this to determine the radius of this circle as (7 – 2)² + (15 – 3)² = 13²

After further discussion, students were able to generalize the equation of a circle centered at (h, k) to be:  (x – h)² + (y – k)² = r²

Then students worked in small groups on the vertical white boards to complete the task included in the Shell center lesson: Sorting Equations of Circles 1

I printed and laminated the cards to make them easier to use on vertical dry erase boards and for facilitate discussion.

Finally, students completed the “Going Round in Circles, Revisited” sheet included in the lesson linked above.

7) Find the center and radius of a circle by completing the square

I created a foldable for students to summarize the equation of a circle that included examples of using completing the square to put an equation of a circle into a standard form. We followed this with additional practice.

<foldable below should be printed on legal sized paper> 

Every time we referred back to completing the square I made visual diagrams connecting it back to their initial development of their understanding of how to complete a square. I never stated any shortcut like, “just divide by 2 and square it.”  Students developed a genuine understanding of the process, which will hopefully lead them to increased success as they begin algebra 2 next school year.

Woot!!

Rolling Cups: Modeling in Geometry

The Rolling Cups task from the Shell Center is a perfect geometry modeling project. I use some form of this task every year for the last three days of the first semester as a final project. This task incorporates constructions, similarity, functions and modeling while pre-assessing students readiness for next semester’s content: solids and circles.

Here is this link to the Formative Assessment Lesson

I’ve discovered that this activity is most effective when I have students produce something each of the 50 minute class periods. Over the years, I have been collecting a wide variety of cups from Goodwill, which I keep in a giant tote in the basement of my school.

With finals complete and students’ motivation dwindling, Rolling Cups is the perfect way to make the most of the days right before break. I move all of the chairs and desks out of the way that we have a big open space in the middle of the class. I also make sure students can easily access the dry erase boards on all of my walls to encourage teamwork and collaboration (more on vertical dry erase boards).

Here is how I break up this activity-

Day 1: Experiment

Here are 4 cups. What will happen when I roll them? Which one will make the biggest circle? Which one will make the smallest? Try it.

I hand each student a different cup and this sheet below to guide their thinking and keep them on task, and then I get out of the way.

At some point during this class period I also show students the Rolling Cup Calculator. I put a link in Google Classroom for easy access. Most students use it on their cell phones to try to find patterns.

Day 2: Develop an equation

This is the formula derivation day. I start by not mentioning the cups at all and just playing a quick whiteboard game reviewing similarity.

During this task, I usually have a few students suddenly yell out:

“This is the cup thing!”…and then start sketching cups on their whiteboards and they begin to use similar triangles to determine the roll radius.

Here is a discussion I had with a student, trying to support their thinking:

Other students look at the first group like they are crazy and we just carry on.

Then I have a few students summarize what they’ve noticed from the previous class.  Next I hand out this sheet: side 1 is the original task and side 2 is for students to write a few sentences summarizing their findings, and score themselves. My school has been working to develop a structure and rubric to elicit quality student writing about mathematics. Below is the current format.

As I present this sheet to students and summarize the expectations for the day, I also tell them that I made a deal with another teacher on Twitter and that I will be scanning their work and sending it to this teacher in Ohio.

I make a big deal about them not writing their names on the back of the sheet where they describe their thinking because that is the side I am going to send to Ohio and I want to preserve their anonymity. In return, I explain, the class in Ohio will be sending me their work, which we will look at tomorrow.

The quality of students work is so much better when they think it will be analyzed by someone else. Of course, this is a big fat lie. I don’t have any plan to send their work to another teacher. But they do so well with this added piece of motivation.

Day 3: Critique other students work

This day goes pretty much as described in the original task. Students review the included samples of other students work and analyze it answering the well written questions from the original task linked above.

It is fun for students to see that other students in other parts of the country approached the problem the way they did. They get excited and genuinely interested. They begin to reflect on their approach and compare it to the student work provided. You can see their confidence grow a little when they recognize that their (alternative school) work is just as good, if not better than the work of typical students in Ohio.

A low-tech unit studying quadrilaterals

In an effort to be better at sharing quality basic stuff that works, here’s how I teach quadrilaterals:

I am hesitant to share the files that I use because I’ve borrowed them from all over the interwebs and at this point I don’t even know where to give credit, but here they are!

[10/11/16 update: Most of this came from Elissa Miller. You can find even more awesome geometry resources on her blog.]

I usually start by having students deduce the properties of parallelograms using an old fashioned ruler and protractor. This is because I’ve noticed that students could use the practice. I know there are a lot of quadrilateral discovery activities on Geogebra, but I still think it is occasionally important to practice using different tools.

 

You can download a editable (word) copy of this sheet here.

After this task, I usually have students complete this checklist measuring, discussing and comparing properties of rhombi, squares, rectangles and  parallelograms.

You can download these files: images & checklist here.

After these investigations and discussions, students work in pairs to complete an Always Sometimes & Never discussion of quadrilaterals, described here.

Students also complete the task Complete the quadrilateral developed by Don Steward as described by Fawn Nguyen. This year, I adapted this task into a Desmos activity.

I also include some basic quadrilateral practice, like this assignment. It is just a good, basic, practice that helps expose student conceptions & understanding.

Geometry Planning Guide

Click here to access and comment on the Geometry Planning guide

Units:

1. Constructions
2. Congruence
3. Transformations & Similarity
4. Right triangles & Coordinate Proof
5. Applied Trigonometry & Solids
6. Circles

In the spirit of Geoff Krall’s Problem Based Curriculum Maps, I attempted to organize my geometry curriculum and learning targets along with associated activities, tasks & lessons. In order to keep this as a useful document, I tried to only include the tasks that I have actually used in my geometry classes. I am interested in adding & deleting from this document regularly to keep if useful for me (and hopefully others). I plan to have the second semester completed this summer, as I am trying to develop this as I go this school year. 

[update 7/25/16: It is finally completed!]

I have shamelessly stolen from all over the MTBoS, Math Vision Project, Engage NY & the Unit Blueprints Project and tried to give credit as much as possible.

Please share any criticisms, activities that I should add, activities that are misaligned, etc… in the comments.

Twitter Math Camp 2016: Get Uncomfortable

Debate – Chris Luzniak & Mattie Baker

“My claim is _____, my warrant is _____ .”

Structures:

1. Chalk Talk: Posters with questions on them, students respond by writing, no talking allowed.
2. Talking points: read more here
3. Debate! Argument = claim + warrant
   1. Soapbox debate: provide class with a debatable prompt, and a minute to think. Then student must stand and state their claim and warrant to the prompt. It’s more fun if you randomly call on students.
   2. Always, Sometimes, Never statements: students summarize previous idea, then state their argument.
4. Point-Counterpoint: use would you rather questions. Students must alternate arguments, so they have to disagree with previous person.
5. Table debate: assign student to teams to develop arguments, and then have the teams debate.

How to encourage debate:

• add debatable terms to questions – best, worst, most efficient, should, biggest, smallest, most, weirdest, coolest, always, sometimes, never
• Change boring math into a debate – Given an equation, ask,
  • What is the best way to graph this?
  • Which number would you change to change the graph the most?
  • This graph will never go below the x axis

Full Scale Debate:

Divide the class into 4 teams. Provide students with a carefully constructed scenario and 4 different stance’s to argue (example provided with musician recording contract).

• have a rubric.
• assign students roles (opening argument, , questioner, attacker, defender, closing argument)
• takes about 3 class periods:

1. understand the problem and develop a plan
2. day research & begin calculations
3. finalize arguments

Socratic Seminars:

Students read a variety of texts or resources on a topic, then consider questions in a large group discussion.

examples of questions to consider:

1. What are some strengths and weaknesses of each presentation?
2. When would each text be appropriate to use?
3. What difficulties may students have?

This sounds like a really interesting thing to do in math class. I need to learn more and see it in action so that I can implement this effectively.

Critical thoughts to creating a successful debate culture:

• the accumulation of many intentional, small teacher moves over time sets the culture of student talk
• When you want students to talk to each other, the teacher must SIT DOWN. make yourself small, and not the center of attention. Encourage students to talk to each other. If it is a whole class debate, have the student talking STAND UP. Slowly back out of the center, have students call on their peers.
• Start early
• Keep it simple. Use basic soapbox debate for the first month or two.
• explicitly talk about what active listening looks like – be very specific (not writing, looking at the speaker, knees pointing toward the person speaking…)
• ideally, dedicate about 5 minutes per class 1-2 times per week
• provide structure (argument = claim + warrant ) and verbal cues
• Occasionally, have students do a quick write providing an image and a word bank. This will help students to practice communicating mathematically.

Keynote: Jose Luis Vilson

We need to talk about race with our students and give them a safe space to grapple with their thoughts. In math instruction, the goal is to teach students to grapple with tough problems for which the solution is not already know and work towards a logical and reasonable resolution. This same principal can be applied to social justice issues.

Some questions/statements for students:

• I just want to hear what you have to say
• Why do you feel this way?
• Where is your compassion/empathy?

We need to become comfortable getting uncomfortable and evangelizing for our truths. Avoiding confrontation and being polite can be destructive in the end.

Getting Triggy With It – Kristin Fouss

This session made me think of this Kate Nowak blog post.

She shared a very complete and organized collection of quality, basic stuff. Progressions, lessons, strategies. I can’t wait to use and adapt it for my first year of teaching pre-calc in a while.

Experience Connecting Representations – David Weiss

This structure connects a visual model to more abstract expressions. This could be graphs & equations, trinomials and algebra tiles, quadratic expressions and their factored forms…

Structure:

1. post more equations than corresponding visuals (task is to match the visual to the equation/expression)
2. provide individual think time – What do you notice?
3. Time to discuss with a partner (teacher circulates, listens & asks a pair if they would be willing to present their thoughts to the class)
4. display verbal cues:

Presenter

We saw ___ so we connected ____.

_____ matches ______ because ______.

Audience

They noticed ____ so they _____.

Their connection works because ______.

5. Get presenter’s to the front. One can only speak and the other can only point. They explain their thinking for one pair. Keep this light, safe & fun. If a student does not explain clearly enough or missing key elements, just let it go, they will most likely come out in later explanations.

6. Ask a student in the class to re-explain the presenter’s thinking

7. Teacher record thinking while a new students explains.

Repeat from step 5 with a new pair of students.

Once all problems have been paired and described by the class, have the pairs try to create a visual mode for the remaining equation that was not paired to a model

Close by having students complete a written reflection.

Explore Math – Sam Shah

Sam talked about a low stakes high reward assignment that he gives his students. They have to complete 4 or 5 mini explorations on any math topics of interest to them (with incremental due dates) and complete a brief written description or some evidence of what they did.

A blog post about it

Site of suggestions

Johnathan Claydon – Varsity Math

He turned the advanced math classes into a ‘club’ called varsity math and created t-shirts, stickers, party’s and a summer camp to go with it. He also made recruiting posters and placed them at the middle schools in order to motivate students and create a buzz around taking more advanced math classes.

This is a great idea! I recently convinced 10 students at my school to take a more advanced math class and I think I will have to figure out how to adapt this concept to fit my tiny group in an effort to get this group to grow in future years.

Tracy Johnston Zagar’s Keynote – Link to slides

She opened my eyes to recognizing the different skill sets that elementary and secondary teachers have and the importance of valuing these skill sets and why we should try to break down our comfort barriers to get over ourselves and learn from each other.

I think I need to write a whole additional blog post on how individuals’ comfort seeking needs really limit our happiness, growth, empathy and success. (an ongoing theme this conference)

Variable analysis game – Joe Bezaire

The math game with the lame name

The basics of how it works:

1. Students guess the rule then they add a line of values that matches the rule.
2. Then these students become judges and let their peer know if they got it too.
3. Write it as an expression. Make connections between the various student expressions.

This may be a good warm up activity, so I want to be sure to link to it here so that I can find it in the future.

Six Steps to Modeling – Brian Miller & Alex Wilson

 

Image from this Dan Meyer blog post

 

1. Define the question
2. Identify Variables & assumptions
3. Develop Model
4. Test Model
5. Adjust / Improve Model
6. Report out

Moody’s Math Modeling Guide – Free Download

In this session we progressed through these steps to develop a model for ranking roller coasters, but the big idea here is more about how to facilitate this process. It would apply well to geometry tasks including 3 act’s such as best square or Mathalicious’ Face Value (my post on this task).

More than Resources – Dylan Kane’s Keynote

Clever Ideas ≠ Coherent Curriculum

We need to be thoughtful and intentional, not just resource collectors.

This resonated with me as I am an avid idea collector, but I struggle with how to make a curriculum coherent. I want to work on criteria for coherence and re-evaluate the content of my current classes.

 

Analyzing Triangle Congruence with AngLegs

I’ve tried to explain why AngLegs are a must have for high school geometry and should not only be considered a tool for younger students. Here is an example of how I find them indispensable in teaching triangle congruence. This lesson is adapted from MARS: Evaluating Conditions for Congruency.

---

“Ok class, you are sitting in pairs and at each table is a bag of AngLegs. On the board I have written the question we are trying to answer for each of the scenarios I will present.”

“I made a triangle that includes a blue AngLeg. Can you make a different triangle that also has a blue AngLeg?”

“Make one. Hold it up.”

“How do you know that these triangles are different?”

“So, you are saying that keeping one side the same does not mean that the triangles must be congruent.”

---

Next, lets look at Card 3:

 

“I made a triangle out of a blue, a purple and a yellow AngLeg. Can you make a different triangle using the same three AngLegs?”

“What if you put them in a different order? …or move the purple between the blue and the yellow? Are you sure they have to be the same? How can you tell?”

Student:  “The triangles still fit perfectly on top of each other”.

Student: “If the three sides on one triangle are the same as three sides of another triangle, then the triangles must be the same.”

---

Look at Card 7:

“How can you tell if an angle is the same in two different triangles?”

Student: “They fit perfectly on top of each other!”

“Is there a way to make these triangles so that they are not congruent?”

Student: “No way. These have to be the same”

Student: “Wait! I made two different triangles with all three angles the same and one side the same.” Does this count? Look!”

Student:”If two angles are the same, then the third angle always has to be the same because they add up to 180 degrees!”

“So what is the conclusion for this one?”

Student:”The triangles can still be different sizes, but their angles are all the same.”

---

“For the remainder of this class period, individually analyze card 5 and any other card, so 2 additional cards. Take good notes and write down your conclusions for tomorrow, where you will be randomly assigned a partner to complete the triangle activity. ”

---

From here the lesson continues as described in the SHELL center teacher guide linked above and described further in a blog post here.

Removing the hurdle of constructions allows students to focus on the learning goal for this activity: determining the minimum information required to guarantee triangle congruence, and what congruence means. It also connects nicely to congruence proofs through transformations as students are physically checking of the triangles fit on top of each other.

Painless Proofs!

Last year I didn’t really teach proofs in geometry. It seemed so procedural and I knew it would take time away from more productive problem solving tasks.

I felt guilty for not including proofs in enough detail and I decided that this year I was going to teach it well.

Here is what I did:

1. Our unit began with the Shell Center task: Evaluating Conditions for Congruency, I don’t always follow these lessons exactly as described, but we focused on the Must the Two Triangles be Congruent? part of this lesson. I found that this activity is much smoother and more effective when using AngLegs instead of trying to draw each triangle (described here and here).
2. After this task we formalize our findings in our notebooks documenting which combinations guarantee congruent triangles [SAS, SSS, ASA, AAS] and which do not [SSA, AAA].
3. Next students practice determining if pairs of triangles must be congruent based on the information given. I am careful to include a few with overlapping triangles and triangles who share a side or contain vertical angles to generate observations and class discussions. At this point I address the reflexive property and vertical angles as reasons sides or angles may be congruent. I follow up any student observations of congruency with “How do you know?” or “Explain why you decided these two angles must be the same.”
4. Review definitions of midpoint, bisector, perpendicular, then a few images where I ask if you are given this information, what can you conclude is congruent. See the interactive notes here. This is the day students complete their first few **Really Basic** congruent triangle proofs.
5. Prior to this class I printed Proof Blocks on colored paper and laminated them, then I used masking tape to affix them to  whiteboards. Once class began I randomly assign student pairs and had them work on a wall mounted white board (Vertical non-permanent surface) with a set of Proof Blocks at each work space.

.

Next I project a proof and students copied the image onto the whiteboard, then marked the givens, saw what else they could determine was congruent, and decided if they had enough information to conclude and prove that the triangles must be congruent.

In order to make sure all students got timely feedback and to hold them accountable, I gave each group an index card and when they finished a proof I would check it. Once it was done well, they got a stamp on their card. At the end of class they turned in their index card with their names & stamps on it, similar to the review activity I described earlier.

I returned to this format with the proof blocks and different pairs about once per week after learning and incorporating new skills. The second half of the slides above were from a day after learning and practicing angles formed by parallel lines & a traversal. I intend to create new “blocks” as we advance through the school year. Next week students will prove that all triangles have a sum of 180 degrees and that base angles of isosceles triangles are congruent using the same format.

With students standing at white boards, they can glance around and see their peers work easily, they are more likely to collaborate, and the whiteboard & Proof Blocks make it much easier to adjust their work when there are any corrections required.

I just graded students quizzes over this unit and it is the first time in my 12 year teaching history that they did very well on the first attempt!

Constructions was MUCH better this year!

Last year I wrote a post about how I wanted to improve my teaching of geometric constructions this year.

This year, I re-read it and used it to help plan this unit better. I never provided the students with steps to make constructions! It was tempting, but I resisted the urge, and they did great!

Here is the sequence that I followed and plan to use next year:

Day 1 – Play with http://sciencevsmagic.net/geo/ see how many of the challenges you can complete. I then had students submit a screen shot of their completed challenges through Google Classroom.

Day 2 – I assigned the construction design project described in my previous constructions post (and linked below). [credit for the designs: Mr. Baroody]

I gave the students compasses and paper to experiment and relate this to the computer task yesterday. They had to complete this at home. There was no discussion of “constructions” just making designs precise and accurate. Here are some students final designs:

[editable first page]

[images]

Days 3/4 – Working in pairs, students alternated roles for each level of Euclid, the game with one student operating the laptop and the other writing down the steps they used to complete each level. We only completed up to level 6. These steps became their notes for constructions.

(Note: there is a geogebra constructions tutorial here.)

Day 5/6 – Construction station rotation – I randomly assigned groups and students rotated with their groups through different stations completing paper and compass constructions, using Popsicle sticks as their straightedges, so they couldn’t rely on measurements. They used their notes that they developed from playing Euclid the game. Sometimes they noticed that their notes were not sufficient, but since they had new partners, they would compare and add notes & diagrams as needed to improve their descriptions.

Day 6 – Constructions extensions. I asked them to apply their knowledge of constructions to new tasks, such as finding 1/8th of a segment, constructing a equilateral triangle and constructing a rhombus.

Students were so much more proficient at using a compass than at the end of this unit last year!

I think I need to develop more construction extension challenges to build on their basic skills next year. I may make a list of challenges and assign point values to them and then assign a total point value that they can get a variety of ways.

Please comment with any ideas to improve this sequence of tasks as an introduction to constructions that builds student confidence while supporting their creativity and problem solving.

Talking Points as End of School Survey

At the end of last school year I had students complete a survey to help me improve, but it took a long time and I think students just started clicking anything towards the end because it was the end of the school year and they were just done.

This year, I decided to use talking points in lieu of a end of school year survey. Hearing their discussions gave me better feedback on what they thought about the class and what they learned during the class then the survey from the previous school year. I’m considering doing talking points as a sort of informal pre / post test at the start and end of each unit.

Here are my talking points for Geometry and the results:

I also listed the major (and memorable) tasks that we did all school year and asked students to identify the activities that were their favorite, least favorite and the ones where they learned the most. It was a good way to have students discuss and recall the activities that we completed throughout the school year. Here are these results:

Kahoot is popular and students like the interactive notebooks. I’m surprised how many students claim to have learned a lot from the Surface area with Doughnuts activity. It is also obvious that students appreciate activities involving food.

Sub (Guest Teacher) Plans

I hate having a sub. I hate missing time with my students. My stepdaughter is pregnant and she is due in about a month. I will be there. I know I’m going to have little notice & ill need a sub, so I decided to put together a few days worth of plans over the holiday break. All of it is created by others, none of it is mine, but I thought I’d put it out there anyway as substitute teacher options.

1) Congruent Halves – Fawn Nguyen

This is a challenging task. It may even require 2 class periods. It is self checking, self explanatory and great use of geometry students time. Requires application of congruence and transformations.

2) Intro Proof Axiomatic System – Justin Lanier

This set of activities requires students to use a set of rules to change a word into another word, and then to create their own axiomatic systems. This gets to the heart of geometry in a non intimidating way.

View this document on Scribd

3) Four 4’s & Foxy 5’s

We have done some four 4’s as a warm up and It is clear that students could benefit from a class period (or more) of this. It allows for collaboration and it is easy enough for students to monitor their own progress. The Foxy 5’s I found recently on my idol, Fawn’s blog here.

View this document on Scribd

I am getting each of these copied, and am writing up instructions and keeping them in a convenient place for the next semester. In my 10 years of teaching I have never had emergency lessons ready to go.  Now I have to resist the urge to use them ASAP because they are awesome tasks, and enjoy being prepared for anything!

What do you have your students do when you are gone?

[update 4/1: there is a great collection of sub plan ideas here]