Constructions was MUCH better this year!

Last year I wrote a post about how I wanted to improve my teaching of geometric constructions this year.

This year, I re-read it and used it to help plan this unit better. I never provided the students with steps to make constructions! It was tempting, but I resisted the urge, and they did great!

Here is the sequence that I followed and plan to use next year:

Day 1 – Play with http://sciencevsmagic.net/geo/ see how many of the challenges you can complete. I then had students submit a screen shot of their completed challenges through Google Classroom.

Day 2 – I assigned the construction design project described in my previous constructions post (and linked below). [credit for the designs: Mr. Baroody]

I gave the students compasses and paper to experiment and relate this to the computer task yesterday. They had to complete this at home. There was no discussion of “constructions” just making designs precise and accurate. Here are some students final designs:

[editable first page]

[images]

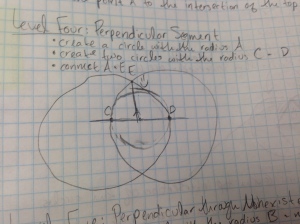
Days 3/4 – Working in pairs, students alternated roles for each level of Euclid, the game with one student operating the laptop and the other writing down the steps they used to complete each level. We only completed up to level 6. These steps became their notes for constructions.

(Note: there is a geogebra constructions tutorial here.)

Day 5/6 – Construction station rotation – I randomly assigned groups and students rotated with their groups through different stations completing paper and compass constructions, using Popsicle sticks as their straightedges, so they couldn’t rely on measurements. They used their notes that they developed from playing Euclid the game. Sometimes they noticed that their notes were not sufficient, but since they had new partners, they would compare and add notes & diagrams as needed to improve their descriptions.

Day 6 – Constructions extensions. I asked them to apply their knowledge of constructions to new tasks, such as finding 1/8th of a segment, constructing a equilateral triangle and constructing a rhombus.

Students were so much more proficient at using a compass than at the end of this unit last year!

I think I need to develop more construction extension challenges to build on their basic skills next year. I may make a list of challenges and assign point values to them and then assign a total point value that they can get a variety of ways.

Please comment with any ideas to improve this sequence of tasks as an introduction to constructions that builds student confidence while supporting their creativity and problem solving.

Maybe constructions will go better next year

This year in geometry I started teaching constructions by having students fill out a foldable using instructional videos as a reference.

By doing this, I made several mistakes. Students saw constructions as an annoying set of steps to memorize and repeat. Most students (as well as the Khan Academy) completely missed the point of using geometric relationships and logical reasoning as a tool to create complex, accurate drawings.

Next year I plan to re- sequence the lessons to support understanding first:

1. I will allow a few DAYS for students time to play with the compass first. To notice, to wonder.
2. I will create an environment for them to talk to each other using the vocabulary we just learned to communicate and try to create this
3. I will make sure patty paper  is available at all times.
4. I will assign this project during the first few days of school to motivate students to get proficient using a compass: 
   View this document on Scribd
   (you can download this file here, if you don’t have a Scribd account)
   

   

   

   
5. I need straight edges without measurements on them so that students have a reason to use a compass instead of a ruler.
6. I will not immediately provide steps to make constructions. I will challenge students to complete a few basic constructions by hand to teach the intent of constructions
7. We will play Euclid, the Game!
8. I plan to still use a foldable for constructions next year, but I’ll have students complete each set of instructions as they conclude how to draw it themselves.
9. I will buy 10 dry erase compasses to encourage student collaborations using my big white boards.
10. We will incorporate constructions as we move toward transformations. for example: when students figure out how to construct a perpendicular bisector, they should also use it to construct a reflection:  

Basic Geometry Constructions 4-tab Foldable

[update: 10/05/15: I no longer use this in my classes because I developed a better sequence of lessons for teaching geometry where students deduce each construction using reasoning instead of copying steps from a website or myself.]

Following an activity developing definitions in geometry, the first major unit of geometry will be constructions.

I plan to take 2 class periods to complete this foldable for their interactive note books with time for practice.  Each tab has space for both the steps and an example for segments and angles, except of course the last tab which contains constructing a line parallel to another line through a point and constructing a perpendicular line.

Instead of just talking at my students, I’m considering having students complete these notes in pairs using this website for directions: http://www.mathopenref.com/tocs/constructionstoc.html

Then I can circulate and provide support as needed. I’ll update this post after using this with students reflecting on its usefulness.

View this document on Scribd

Day 155 & 156: The Triplets of Cellville

I chose this Mathalicious lesson because we have not used circles enough in my geometry classes. We stared the school year with constructions, but haven’t used them much this semester and I wanted them to recall and extend prior learning. I also wanted students to gain more experience modeling real world scenario’s with mathematics & I thought this task would be engaging do to it’s relevance to students lives.  I started off showing the introductory video clip which is a news story of a woman explaining how photos taken with a cell phone include GPS data and how your cell phone records your location. I was surprised that ALL of my geometry students were furious at this video. They thought this lady was dumb for being surprised because “…everybody knows that you can turn on and off the location settings on your phone!” one student argued that if this woman in this video was her mother, she would be furious at her for being so clueless. It was great because it got very intense, and I had no idea how savvy students are with their cell phones. After this discussion died down students inevitably asked: “Wait, what are we doing today? Are we learning how to stalk people with their phones?” and “Mrs B, you are so weird.” Also “This is going to be awesome!” They were hooked.

I don’t want to describe the entire lesson in too much detail because I want you to support Mathalicious and their quality activities, but students constructed circles on a map to determine possible locations of a person in relation to a few cell towers. The lesson also discussed coverage vs locate-ability and students had to use estimation & area formulas in order to draw conclusions and also to determine and justify where they would add a cell tower in a city if they were in charge of making the decision. The only thing I would change for next school year is that I would modify the lesson to use our town and cell tower locations locally to make this more relevant and less hypothetical. Students were engaged and it was a good way to use student interest and incorporate modeling at the end of a school year when motivation is typically pretty low.