Anxiety, Mindset, and Motivation

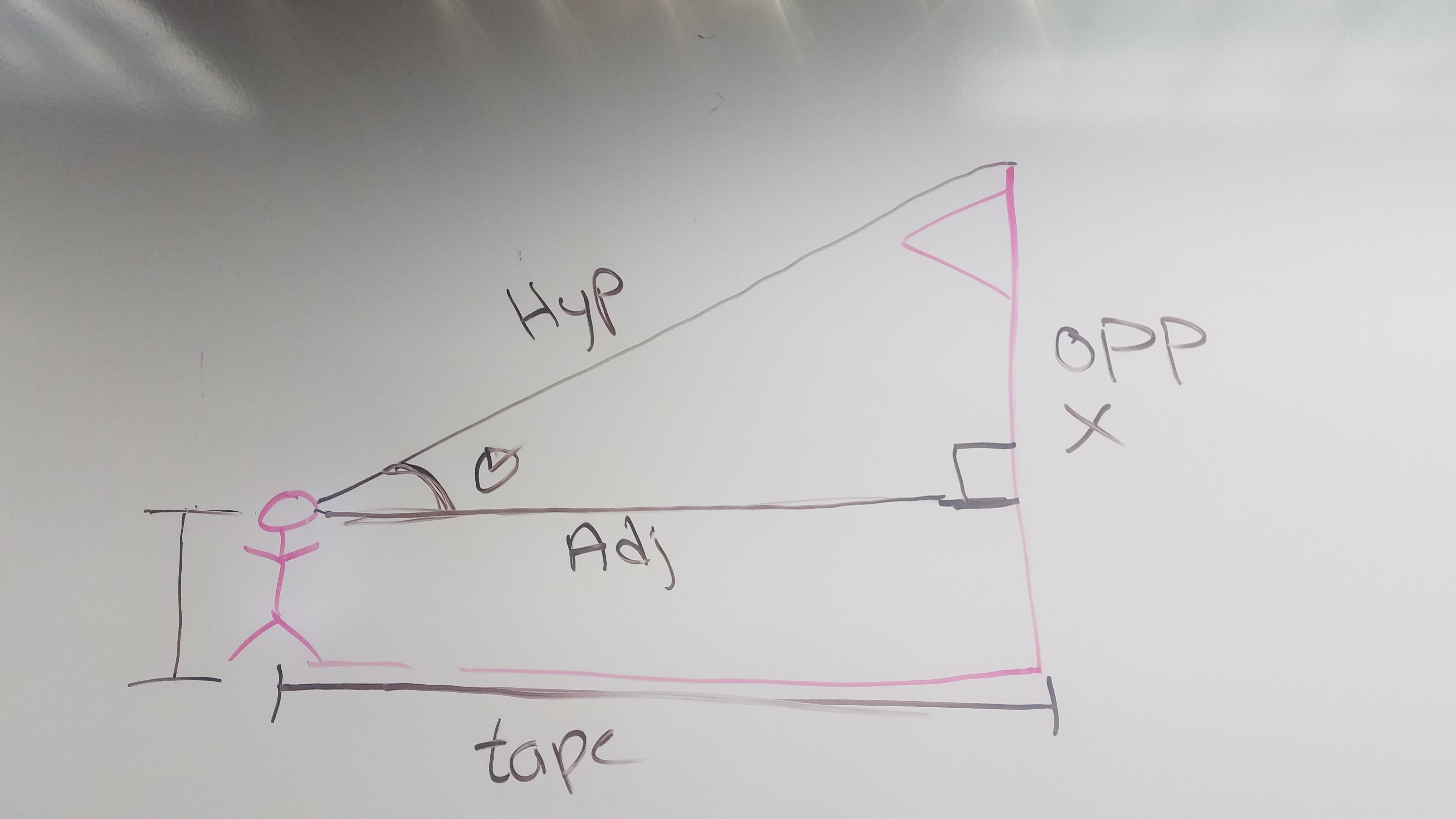
On growth mindset

If we are telling students that it is important for them to develop perseverance and grit or grow new dendrites to get smarter, but the system remains stacked against them, is that really a healthy perspective to promote? From the point of view of students of color and historically looted students, does that just sound like a new version of “pull yourself up by your bootstraps”?

Gutierrez, Political Conocimiento for Teaching Mathematics

“Our brain grows when we make mistakes” is not a helpful message for students. The majority of the time, these student aren’t making mistakes, they are building understanding. Rough drafts are not mistakes and classifying student thinking as a mistake can distract us from what students actually do understand.

Compounding this difference of perspective about growth mindset is our focus on time. We are used to disequilibrium being resolved in a 45 minute class period, or an episode of our favorite sitcom, or between the warm-up and the cool-down, or the pre-test and the post-test. We grow slowly and continuously over time – through consistency and revisions to our thinking mixed with reflection and experience

Growth mindset can be constructive, provided that we recognize its limitations. Instead of telling students their brain grows when they make mistakes, we need to support students in making revisions to their thinking, build from their strengths and enable them the time and support for all students to see and believe in their own brilliance.

How can instructional routines help?

In my early years of teaching, I became aware that my default way of functioning as a teacher was closely aligned to what I experienced in my time as a student. I struggled to try new strategies and get them to stick, being constantly torn between striving to implement new strategies and trying to do no harm to the amazing teenagers under my influence. When trying something new, if it doesn’t go well the first few times, I would resort to more familiar, and less ambitious, methods.

With instructional routines, my students and I committed to working through a set of thoughtfully planned interactions regularly with varying, and carefully selected content. Through this consistency, I was able to reflect and make minor adjustments to the routines – the wording of a question, wait time, when to pair students or allow individual think time –  to make these interactions increasingly effective.

Isn’t this what you think of when you hear about growth mindset? Long term, thoughtful revisions to improve a technique, or approach – not a quick fix of a “mistake.” Let’s model this behavior.

What does anxiety have to do with it?

Being an adolescent is hard. They’re realizing that their parents are not as perfect as they thought, their body is changing, they’re trying to decide how they fit in society and in the social groups at their school. The National Institutes of Health reports that one in four thirteen-eighteen year olds have anxiety, which can be presented as: ADHD, disruptions, off task behavior, shutting down, shouting out, substance abuse, or depression. Understanding the role anxiety plays in behavior is crucial to creating a safe environment.  

Unstructured time and transitions are two primary triggers for students with anxiety. Once anxiety has set in, students working memory declines, making it difficult for them to recall or retain information, initiating a downward spiral for that class period. Routines can be a critical component in preventing the onset of student anxiety and creating a predictable and safe class environment.

Teaching is a stressful job, and anxiety is common among teachers too, impacting our working memory and hindering our ability to be aware of everything happening in our classroom. Like when I am late for work and can no longer remember where I left the car keys, frantically running around the house unable to think clearly. Routines help us too, reducing the cognitive load of every interaction in a lesson and using to a familiar format that’s been adapted to work for your personal style, making space to be able to pay attention to student thinking instead of behavior management.

Bridging from research to action

Thoughtfully selected, developed, or adapted instructional routines, implemented regularly, can help manage student’s anxiety and build on their strengths to authentically develop students confidence and persistence. Over time, teachers build confidence implementing certain routines and student adjust to the expectations of the routines understanding how to find success leading to their development as a mathematician and contributing human being.

I’ll be presenting on this topic with Dylan Kane at NCTM Regionals where we will practice a few routines that allow students to see their own brilliance and discuss many more while considering how they can be adapted to fit your own classroom.

---

Come join the discussion in our session at NCTM Regionals in Seattle:

Anxiety, Mindset, and Motivation: Bridging from Research to Action
November 30, 2018 | 9:45-11:00 a.m. in Washington State Convention Center, 606

Developing a supportive class culture and growth mindset can reduce students’ anxiety, allowing learners to engage thoughtfully with each other around mathematics. Participants will discuss the challenges of shifting mindsets, experience routines as learners and leave with resources and ideas to implement these structures in their classroom.

Too many resources

I was recently asked:

How do teachers make sense of this stuff that gets designed by other people and use it for their own purposes?

I usually take a quick look at the resource and think about if and where it may fit. I may make a note to myself to consider including it when I reach the appropriate part of my school year, and put together a unit plan, then I’ll return to it and consider its appropriateness with my students to achieve a specific learning goal.

There is an abundance of resources available online of varying qualities. I usually do not jump into and investigate a new thing just because somebody pinned it or shared it on Twitter, but I am always afraid I may be missing out on something awesome. I’ve learned that if it is awesome, I’ll continue hearing about it over time and be able to benefit from learning about its implementation in other classes

I am most likely to use a resource either because I learned to know and trust the source, understand the approach and can adapt it to my style and the needs of my students (Desmos activities Shell Centre, Illustrative mathematics) or, because I read blog posts from other teachers discussing how the resource fits in their lesson the strengths and weaknesses of the lesson, what they plan to do next.

As an example: For many years, I heard about a barbie zipline lesson, but I never seriously considered incorporating it into my geometry class until I read a few descriptions of how it worked in other classes. Then I could adapt it to meet my learning goals.

My process when planning a unit:

After developing a list of learning targets for the school year and developing a high level pacing plan, I think about how students make sense of the content, and what content they already know that I can relate it to or build upon. I then sequence the learning targets for the unit. Next, I find, adapt or develop a synthesis project for the end of the unit that incorporates as much of the learning targets as possible from the unit and hopefully also draws in learning targets from previous units & grades too. Rolling cups or spiky door, for example.

After that, I look for hooks. I try to create conditions where students ask me to help them improve at the learning targets I have planned. I try to create a need to learn the thing. After that, I find, adapt, or develop application lessons where they can apply the learning targets as a culminating activity after developing basic understanding of a target – 3 acts and Mathalicious lessons fit well here.

I then lay it all out in a calendar incorporating days for direct instruction, notes, basic practice, and standards based assessments where they are appropriate. I usually build in a few unplanned days in order to allow for some flexibility throughout the unit to make space to dive into teachable moments that may arise.

It is all in the set up: The Waiting Game

It needs to feel authentic

They need to get captured in the intensity of the moment. They need to feel that they are a part of the development of the situation. As much as possible, I need them to ask the questions, not the other way around.

The Waiting Game by Mathalicious

I choose this lesson on Valentine’s day as a preview to our probability unit. The premise of the lesson is to determine how many people a person should seriously date before committing to a partner for the rest of their lives.

The lesson plan as written begins with a very involved handout that lists all of the possible orderings of dating 4 different people: 1234, 1243, 1342, etc… Students are supposed to consider how frequently the end up with their number 1 partner if they choose to commit to their first love compared to if the break up with the first, but then commit to their second person that is a better match than the first, or the third, or wait for mate number 4.

I checked the reflect tab of the Mathalicious lesson to see if there was any thoughts from other teachers:

I thought:

How I adapted the lesson

I did not use the complicated student handout. They need to own this.

I opened the lesson by talking about love. I asked students if they thought they should marry the first person they fell in love with. I showed them some published advice column letters. They debated the advice they would give in each scenario. We talked about the episode of Friends where Rachel and Ross are on a break.

Students had intense opinions.

Quiet students who rarely speak up in math class gave thoughtful reflections.

We invested a good 20 minutes on the buy-in. It got to the point that students were asking; “Is this what we are doing today?” “How is this math?”

Then I asked: “Let’s assume there are 4 people you may fall in love with. If you marry the first person you date, what are the chances that this person is your best match, #1?”

Students replied: 25%

I directed students in small groups to the nearest dry erase board.

What are all of the possible orders that you could date the 4 people? Can you list them?

It started off a complete mess, but eventually groups learned that they needed to organize their thinking.

I followed the rest of this lesson as described in the teacher guide, but using dry erase board and discussion in lieu of a worksheet.

Students calculated the likelihood of committing to their best match if they committed to the first person that was better than their first match. There was some debate and confusion, but eventually students convinced each other that in this case there was a 7/24 chance that you would end up with your best match.

They concluded that the highest probability of ending up with their best match (#1) was if they did not commit to their first love. It was a great Valentines day!

We acknowledged the weaknesses of the initial assumptions and students wrote a reflection on how these assumptions impact our results and weather or not they agree with our conclusions.

 

The great Kahoot workaround

I love getting to learn new teaching strategies through having Eric as an apprentice teacher this semester!

My first period geometry class is very, very quiet. Too quiet. It is a challenge to get any energy and discussion going in that class.

Yesterday, Eric mentioned that he was thinking about trying Kahoot with the class since it can be engaging for students and can increase the energy in the room.  I told him that while I like the program, I dislike that it rewards and encourages speed. I know students are more successful if they take time to think first and don’t just rush to get the best answer.

Here is Eric‘s solution:

1. After logging in to Kahoot, but before the question is presented, tell students to turn their laptops around or put their phones on the table facing down.
2. The question is projected using Kahoot. Students can discuss, but they cannot touch their device while the timer is counting down.
3. Once all students have had enough time to discuss the problem, but before the timer is up, the teacher says GO!
4. Then it is a race to click their solution quickly.
5. Turn devices back around and repeat.

*A modification of this approach using relay races: Have each team place their device along the perimeter of the room, or other side of some line, then have the students stand on the opposite side of the room in their teams. Project the question and once students have had enough time to discuss the solution, yell GO, and a member of each team can race to their device to enter the answer.

So simple and so effective! I am thrilled to be able to use Kahoot again with my students while de-emphsizing speed and increasing student thinking!

School picture day

HEY! YOU – IN THE HOODIE! MOVE TO THE FRONT! YOU’RE SHORT.”

“YOU – GLASSES – MOVE CLOSER TO THE PLAID SHIRT GUY.”

“EVERYONE MOVE IN! IF YOU ARE TO THE RIGHT OF PLAID SHIRT YOU WON’T BE IN THE PICTURE.”

“TAKE YOUR HATS OFF! STOP MESSING AROUND. BE QUIET!”

“TAKE YOUR HOOD OFF! WHAT ARE YOU DOING?!”

I cringe

These are human beings. Stop talking to them like that!

Do I say something to him? Do I leave the room because it is making me so uncomfortable and let it continue?

He is just trying to make our school photo as good as possible. He wants to do the best job he can. He probably works hard.

Do I ever do this?

I might.

We can get so focused on doing our job that we forget that we are working with independent, beautiful, thoughtful, individuals – each with their own stressors and needs and dreams.

This disregard for our humanity happens at every level. We have all been subjected to this and we all have done this to people we care about.

It hurts all of us.

“What you feed us as seeds, grows, and blows up in your face” – Tupac Shakur

Threatening them with a good time

I am terrible at moderation. Terrible.

I’m not sure I even want to be good at moderating.

When I find something I like, I indulge until there is no more.

An example: I tried to make a little geometric art with a compass and straightedge. The next day I was investing too much money and all of my time in compasses, pencils, fancy markers, watercolor paints, brushes…etc. I barely slept for weeks obsessed with making increasingly complex designs.

I teach at a public alternative school. A school where many of my students have struggled with some type of addiction and/or anxiety. My students also struggle with moderation. Impulse control is a challenge for teens because it is a part of a developing teen brain. How can I use this to my advantage?

Why do I need to give them headaches and aspirin in order to generate student buy-in to learning mathematics?

Why not instead make learning math so satisfying that we all want more? Like my experience with Islamic geometric design? Let’s find ways to give learners and their teachers so much satisfaction in making connections and understanding that we all want more.

I propose that we shift our thinking away from, “If Math Is The Aspirin, Then How Do You Create The Headache?” and move towards, “If making connections and discovering is exciting that how do you maximize these opportunities for learners to get them hooked?”

I know it is possible. I have experienced it with my students.

I want to shift perspectives on teaching and learning from headaches and aspirin to connections, discoveries, beauty and excitement.

I need to remember to always invest the time and effort in finding the beauty in a concept for myself and then develop my lessons from this perspective.

Requiring all math to have simple, commercial applications is like requiring all reading and writing to be nonfiction or marketing. Sometimes we want and need fiction and poetry. Sometimes math is just pretty (until you’re ready to do physics with it).

— Jenn Broekman (@jsb16) January 30, 2018

Geometry Right Triangles unit project: Barbie Zipline Day 3

This is the conclusion of a three day lesson applying right triangles. Here is day 1 and day 2.  Eric is my apprentice teacher and he initiated this discussion:

Eric: Yesterday we prepared to go outside, what information did we collect?

student: How much rope we need and what angle.

Eric: Where is the angle? Here or here? What else did we find?

student: The height of the flagpole.

student: The distance away from the flagpole

Eric: One person from each group come up to the board and write your angle and distance from the flagpole on the board.

Eric: Let’s make a plan before we go outside.

We then discussed and agreed that we should actually measure the height of the flagpole  when we put barbie on the pole. We also decided to find the exact ground distance to create a 30 degree angle, but that it looks like it should be approximately 45 feet from the base of the flagpole. Students also agreed that they would like to confirm their thinking that this angle will result in a safe speed for Barbie to zipline down from the top of the flagpole.

 

The Wrap Up

Eric made a sheet for students to reflect on the lesson.

Geometry Right Triangles unit project: Barbie Zipline Day 2

Students sat with their partners from Barbie zipline day 1 and we begin by reviewing the scenario and their calculated flagpole height.

Next we discussed how this zipline will work. I used a string and a binder clip to make a model zipline, using a very steep slope for the zipline and I asked students to predict what would happen if Barbie came down a zipline like this.  They agreed that she would fall too fast and get hurt. Next, I held the string almost horizontal and asked how this zipline would work – and students agreed that she would get stuck or mover too slowly.

I explained that the goal for this day is to use a model in class to determine a plan for Barbie to zipline down safely from the top of the flagpole. By the end of class, students had to know what angle of elevation they planned to use and how far from the base of the flagpole they needed to place the end of the zipline.

This day felt a little chaotic, but students did end up finding errors in their measurements by verifying their calculations in a variety of ways. The worksheet below incorporated a range of geometry topics including:

• Pythagorean Theorem
• right triangle trigonometry to calculate lengths
• inverse trigonometric functions to determine angles
• similar triangles

Tomorrow, we test our calculations outside on the the flagpole.

Barbie is harnessed and ready!

 

Geometry Right Triangles unit project: Barbie Zipline Day 1

I have seen posts about Barbie zipline on occasion over the past few years. I’ve avoided the lesson because it seemed like a lot of advance prep work and typically I don’t allow enough time plan this far ahead and work through constructing a zip line trial run to make sure it all works in advance. To keep it completely real, I also hadn’t seen any description or resources that I thought would fit my classes well. But I found myself approaching the end of a right triangle unit in geometry with 2 full block periods mapped on my unit plan labeled “Right triangle synthesis project – need to create.”

This is my first semester with a full time apprentice teacher, Eric, so I have help and some new motivation to make this a fun project for everyone this time too. This time of the school year, with short days, cold temperatures and no end in sight, it seems a lot of students appear pretty bored with school and many of the staff here are also struggling. I really just needed to lighten things up for the students and myself. The next logical thought: Queue Barbie and high quality pulleys.

Day 1 (80 minutes): How tall is the flagpole?

The set up

Randomly assign teams (I used pairs)

Introduce the activity with this fantastic video from Jed Butler:

We leaned heavily on Jed’s blog post and started with the activity guides included in his post, modifying them a little to incorporate his thoughts on how the lesson could be improved and our learning goals.

1. I like having students select a team name because it forces them to talk to each other before they being working with content. It increases collaboration and breaks down barriers with a safe opening topic for conversation.
2. Given the image below, use Mr. R to estimate the height of the flagpole. This led to students getting rulers and measuring on the image and a rich discussion on whether 4 inches is the same as 0.4 feet. 
   

   

3.   Discussion

1. • Eric: What are some ways we could find the height of the flagpole?
     • student: climb up the flagpole?
     • student: find the angle?
   • Eric: What angle?
     • student: The angle of elevation?
   • Eric: Where does the angle of elevation go (sketches diagram)?
     • student: Do we know how tall Ken is?
     • student: Are we Ken in this situation?
   • Eric: What can we measure?
     • student: You could measure the distance from the flagpole to the person.
     • student: We could use that angle tool thing that Mrs. B carries around.
     • student: oooohhhhhh. yeah.
   • Eric: How could we use that? What else would we need to measure? Would we all have the same measurements?
     • student: The adjacent!
     • student: The hypotenuse!
     • student: oh! So we could use tangent.
   • Eric: I want you to measure two different times, switching roles. Why do you think we should do it twice?
     • student: To see if we get the same answer?
   • Eric: Will we all get the same answer?
     • Student:  No.
   • Eric Why not?
     • student: Because it is not exact, but they should be really close.
   • Eric: Work with your group and make a plan before we go outside.

4.  Measure & Calculate

Outside measurements, then back in for calculations, using this sheet from Jed Butler’s description as a guide.

Favorite question while measuring angles outside:

• student: Is it possible to get the same angle of elevation if may partner and I are different heights?
• Eric: What do you think?

 

5. Enter both of your calculated flagpole heights into the google form (accessed using a bit.ly address from their cell phones).

6.  Justify flagpole height

Project the spreadsheet from the google form as students enter their flagpole heights.

• Eric: We don’t know the actual height of the flagpole. Here are all of your calculated heights. We need to determine what number to use as the height of the flagpole. What are some was to analyze data?
• students: average, mean, median, outliers, graphs, range…..
• Eric:  Determine what height you believe the flagpole is and use one or more of these measures to justify your conclusion.

 

 

Day 2: Design a model and calculate angle of elevation, zipline length, and ground distance.

Definitions in Geometry update

I blogged a few years ago about starting geometry with developing definitions. I’ve made some changes since then, and I have additional ideas for next year that I want to remember.

I’ve found it more useful to start the school year introducing geometry as art, and developing a need for definitions as students struggle to describe the process to create their designs.

Once there is a need for developing agreed upon definitions for terms, I want to use this video to motivate how and why definitions develop:

To make a definition is to highlight and call attention to a feature or structural property. Historically this comes out of working on a problem, not as a prelude to it. The point is you don’t start with definitions, you start with problems. Nobody ever had an idea of a number being “irrational” until Pythagoras attempted to measure the diagonal of a square and discovered that it could not be represented as a fraction. Definitions make sense when a point is reached in your argument which makes the distinction necessary. To make definitions without motivation is more likely to cause confusion.

– Paul Lockhart, Lockharts Lament (p.22)

 

Then, students will develop their own terms and definitions (We ended up with of holes, tubes, and bubbles – you can see the fun thread here.) and we can see how complete it is by trying to classify different objects: a sock? a slice of Swiss cheese? a block of Swiss cheese? etc…

We may engage in some form of Attacks and Counterattacks to help students refine their definitions as the situation requires.

After this introduction of what definitions are and how they work, I will use examples and counterexamples for students to work in small groups and develop definitions of other geometry terms, as described here.