I have been trying to use CPM’s new Precalculus textbook as a guide for my pre-calculus class. During my planing period, I opened to the next lesson to try to put together a plan for my upcoming class.
I only had about one hour to prepare for this class period.
This was the opening prompt:
Gerrit wants to simplify the complex fraction
but is overwhelmed by the fractions within a fraction. Work with your team to help Gerrit write an equivalent expression that is a rational expression instead of a complex fraction. Be ready to share your strategies with the class.
I approached this task thinking about the 5 Practices for Orchestrating Productive Math Discussions. I worked through simplifying the complex fraction in different ways, trying to anticipate different student approaches.
I stopped to think about how this would work with my class:
- I thought back to when I addressed this topic last year – and how poorly it went. Students were frantically writing steps to memorize procedures. Although I am experienced enough to avoid saying “copy-dot-flip” or “invert & multiply“, I know this is how my students learned to divide fractions and it is how they approached these problems.
- I decided I did not want to teach this the same way this time.
- I considered just doing the lesson as described by CPM because I really didn’t have much time to plan and it was good enough. They are HS seniors. I can’t change their perspective on math and learning at this point – right? I tell myself this sometimes. To just keep it simple, but I never listen.
- I read Dan Meyer’s blog post “If Simplifying Rational Expressions Is Aspirin Then How Do You Create The Headache?” I pictured myself asking students to evaluate a complex expression for specific values and whether or not they would be surprised (or even care) if I could evaluate the expression quickly. They have been beaten down by math for most of their lives. I thought this would just be another instance where a math teacher made them feel less competent, and that did not seem like a productive way to pique their interest.
- I thought about when I recently re-read Lockhart’s Lament, especially this part:
“I don’t see how it’s doing society any good to have its members walking around with vague memories of algebraic formulas and geometric diagrams, and clear memories of hating them … Mathematics should be taught as art for art’s sake. These mundane “useful” aspects would follow naturally as a trivial by-product.”
- I thought about Tracy Zagar’s session that I recently attended at ATMNE’s Conference where she talked about how connections through multiple representations made explicit can help students to develop understanding. Tracy also asked participants to think about related topics, often taught separately resulting in learners thinking of math topics as separate concepts. We identified related math topics that are taught separately such as:
- graphing lines: f(x)=mx+b and transformations of functions f(x)=a f(x-h)+k
- similarity and slope
- adding and subtracting
- fractions and division
- I thought about Richard Skemp’s article, Relational Understanding and Instrumental Understanding, and how I could help my students see the simplicity and beauty in simplifying complex fractions.
“There are two kinds of simplicity: that of naivety; and that which, by penetrating beyond superficial differences, brings simplicity by unifying.”
At this point I was losing valuable planning time, but I decided it was more important for me to make sense of dividing fractions for myself, and help students to experience the joy in understanding, than it was to have a flawless detailed lesson plan, so I found and worked through Graham Fletcher’s Making Sense of Invert and Multiply. During my lunch, I created and thought through as many cases of dividing fractions as I could come up with. Then I selected a few to use with my students.
I decided against starting with the opening question provided in CPM’s textbook above, I thought I would close with that question.
I decided to open the lesson asking students to think about and share how they would represent the number of groups of 1/2 that are in 3/4. Instead of beginning my class with these learners feeling intimidated and overwhelmed, they were curious.
Students discussed and compared representations, made connections and got genuinely excited at the silliness of being in a college credit pre-calculus class and that we were making sense of fourth and fifth grade mathematics. Mid-discussion, one high school senior yelled “I am in 12th grade and I just now understand how dividing fractions works!” Shaking her head with a mix of frustration towards how math is taught and satisfaction that she understood division of fractions.
Once they were ready, students worked in pairs on whiteboards to think through CPM’s opening question. They took time, consulted and corrected each other and all ended with the same simplification in different ways. Then the craziest thing happened:
They asked me for more complex fractions to simplify!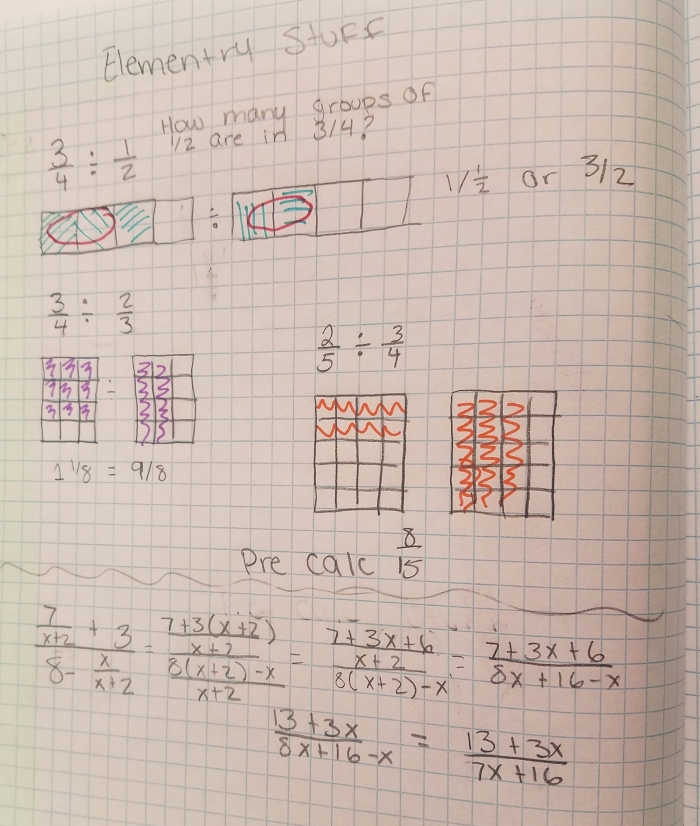

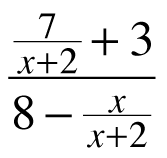
I would love to see more blogging along these lines. It’s a real teaching think aloud, showing how you integrate PD (traditional and self-) into what you’re doing and how it changed things for the learners.
Of course I think understanding division of fractions is a good idea, but why do you think it affected the simplification of the complex fractions which require procedure? Is it just affective – they removed their own fear/anxiety?
I concur, love this kind of thinking blogging. Thank you Lisa!
Hello John! Thanks for the comment!
In the prior class, students practiced adding and subtracting rational expressions, so the “new” challenge they are developing proficiency towards was dividing rational expressions. By making the connection between dividing fractions with and without variables, the process became understandable to them instead of a new set of steps to remember.
Interesting. By defeating the impossibility of understanding fraction division, it opens a whole new area for exploration. Just your comment makes me think that it also changed the setting from procedure to the actual operation of division. I would guess there are very few grade 6-16 learners who think of algebraic fractions as division.
[…] Bejarano’s post Two Kinds of Simplicity offers a useful idea about teaching complex fractions, but much more interesting to me are the […]
Great post! Love how you started with a really low floor (despite many not knowing why dividing fractions works initially) and have them time to make a connection from middle school math to grade 12.
Wondering if there was any connections made between dividing fractions and the CPM question? Did students use the info from the warm ups to approach the CPM question?
Very cool post! I’m totally digging elementary math right now and trying to find was to make explicit connections to secondary math. This helps!
Hi Kyle! I tried to explain the connection between simplifying rational expressions and diving fractions to John in the comment above:
In the prior class, students practiced adding and subtracting rational expressions, so the “new” challenge they would developing proficiency towards was dividing rational expressions. By making the connection between dividing fractions with and without variables, the process became understandable to them instead of a new set of steps to remember.
I am fascinated by elementary math too. Have you read _Knowing and Teaching Elementary Mathematics_ by Liping Ma?
Very cool! It is so hard for people to get the full story from a blog post, especially when the math is constantly becoming more and more abstract as we move through the grades. Awesome stuff.
I haven’t read the book by Ma, but you are not the first to recommend it. Looks like I’ve got another one to add to the list! Thanks for that!
Keep up the great work!
Excellent post, Lisa!
I really like that you shared how you had taught the lesson last year and how students struggled, didn’t really understand, and were engaged by “frantically writing steps to memorize procedures”.
This post also made me think about how challenging lesson planning can be for teachers without as much experience and knowledge about various strategies and resources as you. I’m impressed you pulled all of this off with only one hour to plan.
Keep up the great work!
I loved reading this post about dividing fractions. I teach sixth grade math and think that dividing fractions might be one of the most important “big idea” units we cover during the school year and drawing bar models is a very important part of helping students with conceptual understanding. I like to show the rhyme “Ours is not to reason why, just invert and multiply” and instead ask students to explain why multiplying by the reciprocal give the same result as dividing.
As a further part of the exploration, these complex fractions can be connected to the students’ prior knowledge of equivalent fractions, which rests on the notion that it’s ok to multiply by 1 (because 1 is the multiplicative identity element). So 2/3 x 5/5 (which equals 1) is equivalent to 10/15 etc. Identify the lowest common denominator of all of the fractions present in numerator or denominator of the complex fraction, in this case x+2. So multiply the complex fraction by (x+2)/(x+2). This simplifies the complex fraction to the simpler form that the students arrived at, but avoids the daunting look of the 4-tiered fractions-within-a-fraction.
[…] is posts like Lisa’s most recent one that make me long for more collaboration K-12. I have to admit, when I saw her Twitter post with […]
Just a rich and insightful post! I will be sending the link to the K-8 and HS department heads as we plan for a joint meeting – this is the kind of teacher thinking we should be modeling and sharing.
Thanks, Norma!
As concrete as the division of fractions can be, why do I find myself avoiding them?! All I did was multiply by by one big 1 (x+2/x+2). Am I coming at teaching this topic the wrong way? Even after reading your blog/examples…I would still teach with this method. Granted, I don’t have too many logical thinkers NOW, but I want to encourage logical thought and help develop logical thinkers. I’m a little embarrassed at posting this. But I couldn’t find your email. And I have now spent over an hour of my planning consumed by this blog. Am I missing the big picture?
Great lesson! I feel like it makes the perfect argument for restructuring the “mile wide, inch deep” standards that we teach in high school. In Algebra 2, there is one part of one section of one chapter…Ch. 7.4 example 5 that addresses this. And of course, they are totally going to remember this when they get to pre cal, right??! I would love to have the time to explore more deeply. We need more time!!!! …..is the battle cry of all math teachers everywhere.
[…] I know it is possible. I have experienced it with my students. […]
[…] then lay it all out in a calendar incorporating days for direct instruction, notes, basic practice, and standards based assessments where they are appropriate. I usually build in a few unplanned […]
Thanks for sharing Lisa! I really appreciate the vertical collaboration taking place here because you’ve helped me a lot. My big connection was when you related your understanding back to complex fractions. That was huge for me to see and makes much more sense.
I’ll take any more connections you make. Cheers!
As a third year teacher who took a 3 year break from teaching and just this year is back in the classroom, this was so validating. I have an MA in math education and spend a lot of my planning period mentally rotating between teacher adapted curriculum, CPM, district curriculum, things I’ve learned in PD, knowing my students, etc. I often do a lot of thinking and changing of my ideas and only in the last 20 minutes pull something together that makes sense to me. I always wonder if I’m wasting time, but you make me realize that this thinking is the work of teaching and that I’m spending the time consulting whatever expertise I do have.
Thank you so much for this comment, it made my day!